Classification Of Optimization Problems

Viewed 21 times 0 begingroup when i do some exercises of optimization i always run into some defined problems like qp quadratic programming cclp chance constrained linear programming and so on. I want to know how to find the standard of classifying different optimization problems and also why. An optimization problem with discrete variables is known as a discrete optimization in which an object such as an integer permutation or graph must be found from a countable set.

fluffy black and white cat with blue eyes ff14 フェンリルマウント gimp cmyk export gimp 2 10 cmyk separate gimp cmyk exportieren gimp bild in cmyk konvertieren find modern axe the forest gimp cannot open cmyk psd

4 Classification Of Optimization Problems Neos 2014 Download

4 Classification Of Optimization Problem Ip Integer Programming

3 Classification Of Optimization Problem From Majumdar A Et Al

Classification Of Optimization Techniques Adapted From 4

Classification Of Optimization Problems Ppt Download

7 Classification Of Optimization Problems 28 Download

In mathematics computer science and economics an optimization problem is the problem of finding the best solution from all feasible solutions.

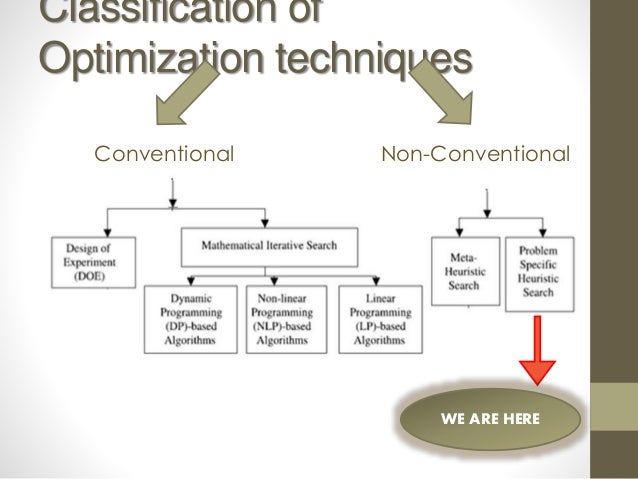
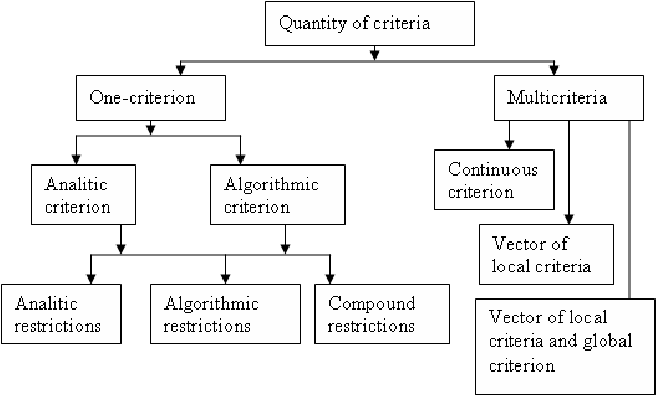
Classification of optimization problems. Ax b and x 0 3 non linear programming nlp objective function or at least one constraint is non linear. A set of variables that encode decisions to be made. By looking at the different optimization opportunities at the different stages of the service life cycle one can differentiate between design time optimization deployment time optimization and. Which forms the basis for the classification into subcategories.

Constrained optimization problems can be furthered classified according to the nature of the constraints e g linear nonlinear convex and the smoothness of the functions e g differentiable or nondifferentiable. An optimization problem typically consists of the following. 11 minimize ψ ω i 1 i g i ξ i subject to 12 y i ω x i β 1 ξ i i 1 i 13 ξ i 0 i 1 i 14 ω r p 15 β r where ξ ξ i r i is the vector of deviation variables and for each i i g i the loss function is convex and increasing in r. None one or many objectives.

Ask question asked 15 days ago. Classiﬁcation of optimization problems common groups 1 linear programming lp i objective function and constraints are both linear i min x ctx s t. Ax b and x 0 2 quadratic programming qp i objective function is quadratic and constraints are linear i min x xtqx ctx s t. For all subcategories with one exception optimization is performed during operation of the relevant cloud and or fog services.

None one or many objectives. Constrained optimization problems can be furthered classified according to the nature of the constraints e g linear nonlinear convex and the smoothness of the functions e g differentiable or nondifferentiable. Active 14 days ago. The classifier is found by solving the following optimization problem.

Functions optimization problems can be classified as separable and non separable programming problems i separable programming problems in this type of a problem the objective function and the constraints are separable. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. A problem with continuous variables is. The exception is subcategory 3 4 distributing physical resources.

Classification of optimization problem.